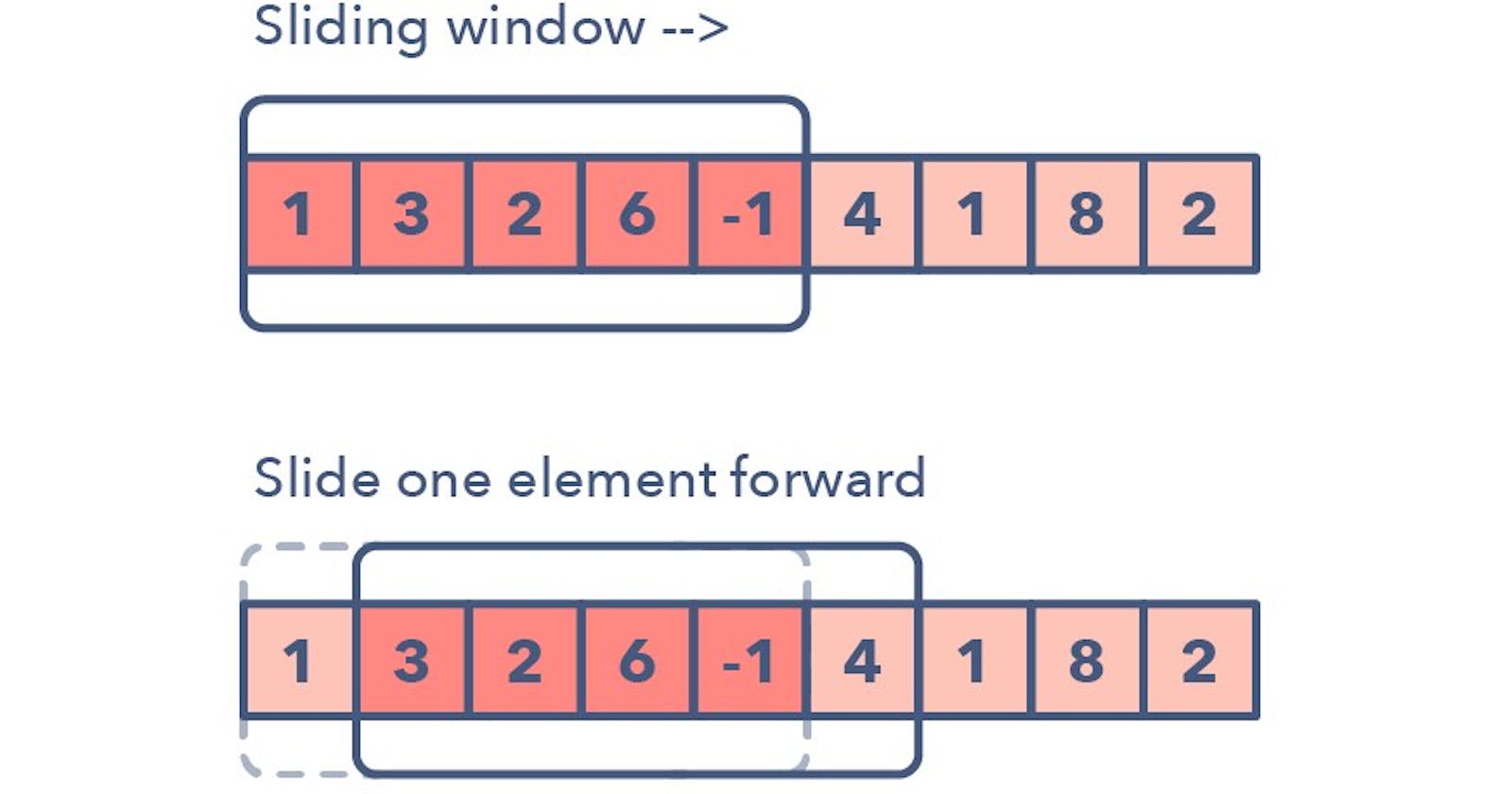
In this blog, I aim at explaining a very popular coding interview question to my readers, commonly known as Sliding Window Maximum, this formally goes like this
Given an array A and an integer K. Find the maximum for each and every contiguous subarray of size K.
Sample Input : arr = [9,6,11,8,10,5,4,13,93,14], window_size = 4
Sample Output : 11,11,11,10,13,93,93
I would be touching upon all the ineffective approaches, but would no go in depth for those.
Naive Approach
Just run a loop from position 0 to position n-k, for each position just consider the subsequent subarray of length k and then calculate maximum. The complexity for this approach would be O(n log (k)). This is very similar to a sliding window protocol, and then calculating maximum for each window.
Using Self Balancing BST
This is another good try. Pick the first K elements and add it to an BST. Run a loop for i = 0 to n – k
- Get the maximum element from the BST, and print it.
- Search for arr[i] in the BST and delete it from the BST.
- Insert arr[i+k] into the BST.
Again this would cost us an overall runtime of O(kLogk + (n-k+1)*Logk) which is asymptotically O(n log (k)).
Using Deque
A deque is a double ended queue, a very interest modification of a simple queue, thus supporting insertion and removal at both ends (front and rear). The idea is to not recompute the maximum for each window again and again. The algorithm can be divided into two major steps.
Stage 1
Add the first K elements in the Deque
- Define the deque
- For i = 0 upto K-1
- (i) Remove all elements from the rear of the Deque which are less than current element (arr[i]), this is because they would never be used for this window or upcoming windows.
- (ii) Add the index of the current element (i) to the Deque
At the end of the first stage it is very clear that our deque will contain a monotonically decreasing sequence (i.e. arr[i] >= arr[i+1]). Another observation is that, the first item at the front of the deque is the maximum for the first window.
Stage 2
Add remaining N-K elements in the Deque Remember, we need to maintain the size and order of elements in the deque. At any point of time it is always a monotonically decreasing sequence inside the deque.
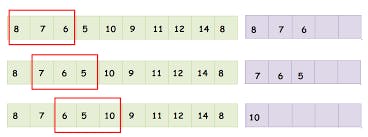
- For i = K upto N-1
- (i) Dequeue the item at the front, it is the maximum of the previous window. You can print it or store it.
- (ii) Remove the elements from Deque, that do not belong to the current window from the front. Elements should be within the range
(i-k)+1 upto iotherwise just remove from the front. - (iii) Remove all elements from the rear of the Deque which are less than current element (arr[i]), this is because they would never be used for this window or upcoming windows.
- (iv) Add the index of the current element (i) to the Deque
- Finally, after the loop --- Dequeue once from the front to get the maximum of the last window.
Example Dry Run
- Input =
arr = [9,6,11,8,10,5,4,13,93,14], window_size = 4 - Initially
deque([]) - Add 0(=9) to deque, followed by 1(=6), thus
deque([0, 1]) - 11 is greater than 6, 9 thus they are removed. Now
deque([2]) - Add 3(=8) to deque, thus
deque([2, 3])
Thus, the first K elements have been processed.
- Adding element 10 will result in removal of element 8. Thus current state becomes
deque([2, 4]) - Add 5(=5) thus
deque([2, 4, 5]) - Before adding 6(=4) we need to clean up the Deque, remove the elements which do not belong in this window. Thus remove index 2 from the Deque. Then add index 6 (=4). Thus
deque([4, 5, 6]) - Adding 13, the previous elements are all smaller than it. Thus they will be removed. Thus
deque([7]) - Similarly, 93 is greater than 13 (which is the only item in the Deque), thus will be removed. Therefore,
deque([8])
Note that, at each state of the Deque, the first element is the maximum of the previous window, thus we keep collection the maximums from the front of the Deque as we slide it through the array.
Code

Clearly, the runtime for our code is linear, that is O(n). This can also be implemented using a stack instead of a Deque as well. Check this post for more details.
An alternative version of this problem is the Sliding Window Minimum. I would suggest you to think on what modification we need to the above algorithm solve that problem.
This problem has been asked in coding interviews for several top tech companies like Google, Amazon, Facebook, Flipkart, Uber, Walmart,Directi, SAP Labs, etc.
Good luck for your interviews!
I hope you learned something from this blog if you followed it carefully. As a reward for my time and hard work feel free to buy me a beer or coffee.