What is a Maze Runner?
According to Wikipedia, in electronic design automation, a maze runner is a connection routing method that represents the entire routing space as a grid. Parts of this grid are blocked by components, specialised areas, or already present wiring. The grid size corresponds to the wiring pitch of the area. The goal is to find a chain of grid cells that go from point A to point B.
Simple Idea
Assume that we have a matrix and some of the cells are blocked, thus we can neither go through them or over them. We have a source point in the matrix grid and a destination point. We need to calculate the minimum number of steps required to reach the destination, starting from the source given that we cannot move diagonally. The only possible moves are:
- Adjacent Left
- Adjacent Top
- Adjacent Right
- Adjacent Bottom

Quite simple, huh!
Maze Solving Algorithms
Although we have several popular maze solving algorithms, thanks to computer scientists, yet solving mazes efficiently is quite an area under research even today.
According to Wiki, there are a number of different maze solving algorithms, that is, automated methods for the solving of mazes. The random mouse, wall follower, Pledge, and Trémaux's algorithms are designed to be used inside the maze by a traveler with no prior knowledge of the maze, whereas the dead-end filling and shortest path algorithms are designed to be used by a person or computer program that can see the whole maze at once.
One of the simplest methods that I found dead easy to get a grip on is the Lee's Algorithm. It uses a wave propagation style (a wave are all cells that can be reached in n steps) throughout the routing space. The wave stops when the target is reached, and the path is determined by backtracking through the cells.
Lee's Algorithm
The Lee algorithm is one possible and easy solution for maze routing problems based on breadth-first search. It always gives an optimal solution, if one exists, but is slow and requires considerable memory. It is highly applicable in global routing and detailed routing.
The time and space complexity is of the order O(m x n), i.e the size of the grid.
Alas! :(
Although, we can somewhat reduce the time by making a few optimizations such as halting the algorithm when we reach the destination and more.
Let us have a look at the algorithm, after which we shall implement it in Python (my favourite :P).
Step 1 :
- Initialise start point, mark it with 0 in the **cost** matrix.
Step 2 :
- REPEAT
- Mark all unlabeled neighbors of points marked with i with i+1
- Set i := i+1
UNTIL ((target reached) or (no points can be marked))
Step 3:
- go to the target point
REPEAT
- go to next node that has a lower mark than the current node
- add this node to path
UNTIL (start point reached)
Step 4:
- Block the path for future wirings
- Delete all marks
Visualize The Algorithm
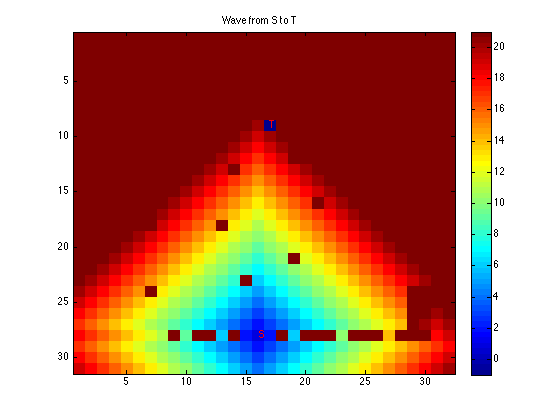
Modified Implementation
I have used two matrix, namely the cost matrix for storing the updated costs and a visited matrix to mark which cells are previously visited and thus marked once atleast. I have used a process queue to perform the recursive operations in a FIFO manner - first the left, then top, then right, then bottom, a simple clockwise approach from the current cell.
Modifications
- Initialise the cost matrix with -1, initialise the visited matrix with False.
- Set cost(start) := 0
- Start from the point, mark it visited and check if Left is valid cell or not, thus add to process queue. Repeat the same for Top, Right and Bottom.
- Perform the first task from the process queue and operate on it in a FIFO fashion until there is no more remaining.
- If we've encountered finish point or destination the halt the algorithm.
- We try to minimise the cost the reach each cell, if such a path is found.
class Solution(object):
def __init__(self, maze, start, finish):
self.maze = maze
self.m = len(maze)
self.n = len(maze[0])
self.start = start
self.finish = finish
#CREATE VISITED MATRIX
self.visited = [[False for i in range(self.n)]for j in range(self.m)]
self.cost = [[-1 for i in range(self.n)]for j in range(self.m)]
#MARK START POINT TO ZERO
self.cost[start[0]][start[1]] = 0
self.visited[start[0]][start[1]] = True
self.queue = [] #PROCESS QUEUE
def dimension(self):
print("Grid Dimensions: ",self.m,"x",self.n)
def isValid(self, x,y):
if(x=self.m or y>=self.n):
return False
elif(self.maze[x][y]=='t'):
return False
else:
return True
def printer(self, mat):
for i in range(len(mat)):
print(mat[i])
print("--------------")
def go(self):
if(len(self.queue)==0):
return
#self.printer(self.cost)
x,y=self.queue[0][0],self.queue[0][1]
self.queue.pop(0)
if(not self.isValid(x,y)):
return
elif(x==self.finish[0] and y==self.finish[1]):
return
else:
self.visited[x][y] = True
# LEFT
if(self.isValid(x,y-1) and not self.visited[x][y-1]):
self.queue.append((x,y-1))
if(self.cost[x][y-1] == -1):
self.cost[x][y-1] = self.cost[x][y] + 1
else:
self.cost[x][y-1] = min(self.cost[x][y] + 1, self.cost[x][y-1])
# TOP
if(self.isValid(x-1,y) and not self.visited[x-1][y]):
self.queue.append((x-1,y))
if(self.cost[x-1][y] == -1):
self.cost[x-1][y] = self.cost[x][y] + 1
else:
self.cost[x-1][y] = min(self.cost[x][y] + 1, self.cost[x-1][y])
# RIGHT
if(self.isValid(x,y+1) and not self.visited[x][y+1]):
self.queue.append((x,y+1))
if(self.cost[x][y+1] == -1):
self.cost[x][y+1] = self.cost[x][y] + 1
else:
self.cost[x][y+1] = min(self.cost[x][y] + 1, self.cost[x][y+1])
# BOTTOM
if(self.isValid(x+1,y) and not self.visited[x+1][y]):
self.queue.append((x+1,y))
if(self.cost[x+1][y] == -1):
self.cost[x+1][y] = self.cost[x][y] + 1
else:
self.cost[x+1][y] = min(self.cost[x][y] + 1, self.cost[x+1][y])
self.go()
def minCost(self):
self.queue.append((self.start[0], self.start[1]))
self.go()
return self.cost[self.finish[0]][self.finish[1]]
s = Solution([['f', 'f', 'f', 'f'],['t', 't', 'f', 't'],['f', 'f', 'f', 'f'],['f', 'f', 'f', 'f']], (3,0), (0,0))
print(s.minCost())
Sample Input
[
[f, f, f, f],
[t, t, f, t],
[f, f, f, f],
[f, f, f, f]
]
Start : (3,0)
Finish : (0,0)
Note: Cells marked with 't' are blocked.
Sample Output
7
Explanation
Final Cost Matrix Looks Like This !
[
[7, 6, 5, 6],
[-1, -1, 4, -1],
[1, 2, 3, 4],
[0, 1, 2, 3]
]
To visualise how the algorithm works, uncomment the third line under the definition of go() function, i.e #self.printer(self.cost).
Hope you enjoyed this problem too, just like I did. This actually appeared as a Google interview problem in the past. 😛
References:

